関節には凹面と凸面が存在する
滑膜関節には、末梢が出っ張った凸面と、へこんだ凹面とで形成されてたものが多く存在します(また、関節面が凹凸になっておらず平坦なものも存在し、それらは『平面関節』と呼ばれています)。
ただし、この凹凸には軟骨部分も含まれての形状を指しています。特に凸側には中央に最も軟骨があり、凹側には端の方に軟骨が多いという特徴があるようです。
そのため、レントゲンには軟骨が映らないので凹凸になっていないように見えることがあるかもしれませんが、実際は軟骨も含めて凹凸である点には注意が必要です。また、骨模型を観察する際も、同様な点に注意する必要があります。
四肢の凹凸の例
四肢の関節面を下記に示します。
| 関節 | 肢位 | 関節 | 肢位 |
|---|---|---|---|
| 股関節 | 寛骨=凹 大腿骨=凸 | 肩甲上腕関節 | 肩甲骨=凹 上腕骨=凸 |
| 脛骨大腿関節 | 大腿骨=凸 脛骨=凹 | 腕尺関節 | 上腕骨=凸 尺骨=凹 |
| 距腿関節 | 下腿(脛骨+腓骨)=凹 距骨=凸 | 橈骨手根関節 | 橈骨=凹 手根骨=凸 |
治療面と並進運動
- 治療面:
- 関節の『凹側の両端を結んだ接線』のこと。
- 並進運動:
- 治療面に対する垂直または平行方向への他動運動。
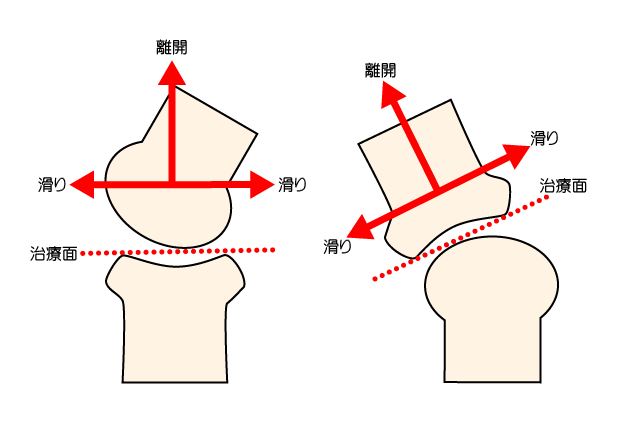
関節副運動テストや、関節モビライゼーションの際は、常に凹面である治療面を基準として並進運動を行う事になります。そして、それぞれ並進運動を他動的に操作する際には下記のように表現します。
- 治療面に対して垂直方向への並進運動⇒離開(or 圧迫)
- 治療面に対して平行方向への並進運動⇒滑り
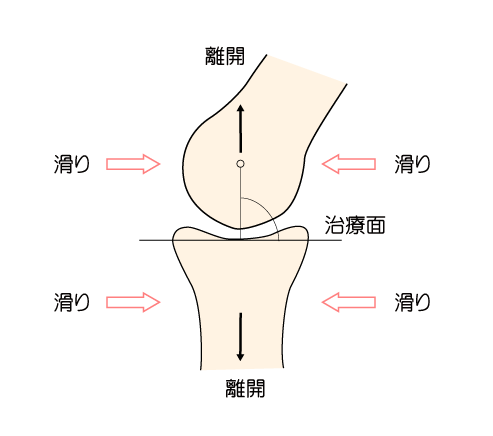
※色々な用語解説にて紹介している関節運動学にも同様に表現される言葉があるので、整理してみてください。
並進運動をする際は下記のポイントを押さえておく必要があります。
- 凸の関節面を固定し凹の関節面へ並進運動を加える場合は、治療面は関節角度によって変化することに注意する。
(例えば、脛骨大腿関節の伸展制限に対して、脛骨を腹側へ滑らせようとする際は、脛骨大腿関節の屈曲角度によって、滑らせる方向も変化する。) - 凹の関節面を固定し凸の関節面へ並進運動を加える場合は、治療面は関節角度によって変化することは無い。
(例えば、距腿関節の背屈制限に対して、距骨を背側へ滑らせようとする際は、距腿関節の背屈角度に関わらず、滑らせる方向は常に同じである。)
治療面を理解・イメージで出来ることが関節モビリゼーションの必須条件となる為、非常に重要です。
凹凸の法則とは
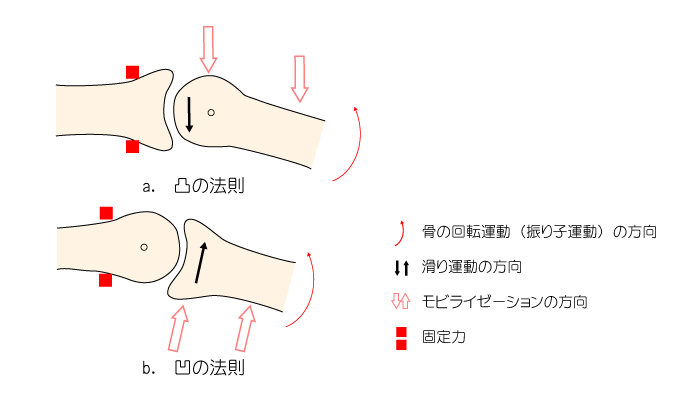
関節運動学では、『自動および他動的な骨運動に伴って生じる関節面の運動』を構成運動と呼び、この構成運動は凹凸の法則に沿った動きになるとされています。
- 凹の法則:
- 凹の関節面が運動をする際は、骨運動と同じ方向に滑りが生じる。
(例えば、脛骨大腿関節の伸展運動の際は、骨運動と同じ方向である腹側へ脛骨が滑る。) - 凸の法則:
- 凸の関節面が運動をする際は、骨運動とは反対方向に滑りが生じる。
(例えば、距腿関節の背屈運動の際は、骨運動と反対方向である背側へ距骨が滑る)
四肢の凹凸を、この法則に当てはめると下記のようになります。
| 関節 | 肢位 | 関節 | 肢位 |
|---|---|---|---|
| 股関節 | 凸の法則 | 肩甲上腕関節 | 凸の法則 |
| 脛骨大腿関節 | 凹の法則 | 腕尺関節 | 凹の法則 |
| 距腿関節 | 凸の法則 | 橈骨手根関節 | 凸の法則 |
上記は必要最低限な情報だが、もう少し詳しく「各関節の凹凸」について知りたい方は以下の記事で詳細をまとめているのでチェックしてみてほしい(理学療法士協会徒手理学療法部門の資料参考)。
凹凸の法則は間違いである?
凹凸の法則を知っておくことは関節包内運動をイメージする上でも、関節副運動テスト時に優先順位を素早く見極めて効率的に介入していく上でも重要な知識と思われます。
しかし、「肩関節の屈曲方向へ可動域制限がある⇒この関節は凸の法則だから○○方向への滑りをもっと引き出してあげれば、可動域が改善されるはず」などと安易に法則を当てはめず、あくまで参考程度に留める必要があります。
なぜなら、関節構成運動は関節面の凹凸な構造だけでなく、関節包・靭帯・筋などの総合的な影響により生じているからです。したがって、これらの組織に機能的・構造的変化が生じているかどうかはもちろんのこと、肢位によっても構成運動には変化が生じる可能性があります。
実際に、関節包内運動を様々な手段で検証できるようになってきた現在において、実際は凹凸の法則通りに構成運動が生じなかったことが証明された研究結果も散見されるようになってきています。
そのため、『凹凸の法則』ではなく『凹凸のパターン』と表現したほうが適切なのではという意見もあります。
※『法則』とは「いつでも、またはどこでも、一定の条件のもとに成立するところの普遍的・必然的関係、またはそれを言い表したもの」である。~広辞苑より~
とにもかくにも、椎間板理論・脊柱組み合わせ運動などと同様に凹凸の法則も『解剖・運動学的な理屈と臨床は必ずしも一致しない』ということは、頭に留めておく必要があると思われます。
大切なのは凹凸の法則への当てはめではなく、評価である
徒手理学療法の世界においても、『凹凸の法則は絶対である』という主張は薄らいできています。
特に肩甲上腕関節に関しては、関節面の構造以外の要素が構成運動に与える影響も大きいというのが世界的な見解であるようです。
何度も重複して述べている気がしますが、『凹凸の法則』という知識を頭に入れておくことは大切ですが、知識レベルのことと実際の評価は必ずしも一致しない事も念頭に入れておく必要があります。
そして、関節副運動テストの結果や、試験的治療で治療効果が得られたかどうかなどを複合的に考えてアプローチするというのが、現在の関節モビライゼーションにおける考え方となります。
凹凸の法則はあくまで『参考』であって、凹凸の法則に沿って関節モビライゼーションを施行する訳では無いのです。
また、余談ではありますが凹凸の法則が正しいかどうかに限らず、各関節がそれぞれ決まった凹凸面で形成されているのは疑いようもない事実です(平面関節や、一部の意見が分かれている関節を除く)。そのため、関節モビライゼーションを『凹面の治療面に対する並進運動』で施行する事は鉄則になります。
関連ブログ記事:肩/肘/手/股/膝/足関節のモビライゼーションのポイント解説
以下のブログ記事では、四肢に対する関節モビライゼーションのポイントを解説しています。
この記事の中で、イラスト付きで『治療面』や『併進運動』についてもイラスト付きで解説しているので、こちらも合わせて観覧してもらえれば、合わせて観覧してもらえれば理解が深まると思います。
スポンサーリンク




